Se llaman ecuaciones exponenciales a las ecuaciones en las que en algún miembro aparece una expresión exponencial.
MÉTODOS DE RESOLUCIÓN:
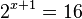
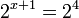
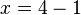
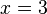

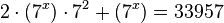
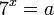
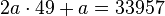

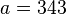
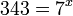
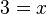
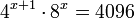
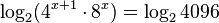
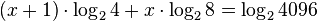
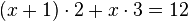
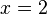
MÉTODOS DE RESOLUCIÓN:
Igualación de bases
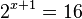
Si el primer miembro sólo tiene un término y el término del segundo miembro es potencia de la base del término del primer miembro, entonces el segundo miembro, se expresa como potencia de la base de la expresión que contiene la incógnita. En el ejemplo 16 es potencia de la base dos de 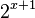 .
.
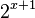 .
.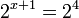
Luego, por la siguiente propiedad: 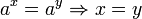 , tenemos:
, tenemos: 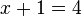
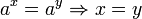 , tenemos:
, tenemos: 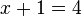
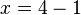
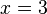
Cambio de variables

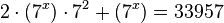
Aplicamos el cambio de variable:
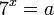
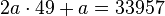
Despejamos a:

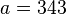
Ahora, recordemos que 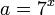 , luego:
, luego:
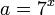 , luego:
, luego: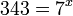
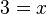
Usando logaritmos
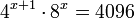
Usamos logaritmo a ambos lados de la ecuación:
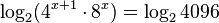
Por propiedades de los logaritmos, tenemos:
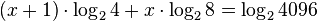
No hay comentarios:
Publicar un comentario