Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A.
En caso contrario, si a no es un elemento de A se denota aÏ A.
EJEMPLOS
Æ : el conjunto vacío, que carece de elementos.
ℕ: el conjunto de los números naturales.
ℤ: el conjunto de los números enteros.
ℚ: el conjunto de los números racionales.
ℝ: el conjunto de los números reales.
U: el conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal
Un conjunto se puede definir:
Por extensión: teniendo todos los conjuntos
Por compresión: mediante una propiedad
Subconjunto: En las matemáticas, un conjunto A es subconjunto de un conjunto B si A «está contenido» dentro de B.
AÍB

UNIÓN: Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B,
A È B := { x | x Î A Ú x Î B}.
PROPIEDADES
Idempotencia. La unión de un conjunto A consigo mismo es el propio A :
- La unión de un conjunto A con un subconjunto suyo B lo deja inalterado:

Propiedad distributiva
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto: A ∪ (A ∩ B) = A
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto: A ∩ (A ∪ B) = A
Cardinalidad
El número de elementos de la unión de dos conjuntos finitos A y B es la suma de los elementos de A y de B, si no tienen elementos en común.

Como en un conjunto los elementos no pueden repetirse, si A y B tienen elementos en común, al sumar sus elementos se contarían los elementos comunes más de una vez.
Por ello, es necesario eliminar las repeticiones al contar los elementos de A ∪ B: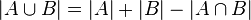
INTERSECCIÓN:
Dados dos conjuntos A y B, su intersección es otro conjunto cuyos elementos, necesariamente, pertenecen a los dos conjuntos A y B.
A Ç B := {x | x Î A Ù x Î B}
PROPIEDADES
Idempotencia. La intersección de un conjunto A consigo mismo es el propio A :
La intersección de A y B es un subconjunto de ambos:
La intersección de un conjunto B con un conjunto A que lo contenga, deja a B inalterado:
Propiedad asociativa: La intersección de los conjuntos A y B ∩ C es igual a la intersección de los conjuntos A ∩ B y C :
Propiedad conmutativa. La intersección de los conjuntos A y B es igual a la intersección de los conjuntos B y A :
Elemento absorvente. La intersección de un conjunto A con el conjunto vacío ∅ es ∅:
Propiedad distributiva
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto: A ∪ (A ∩ B) = A
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto: A ∩ (A ∪ B) = A
Diferencia:
La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.

EJEMPLO: la diferencia entre el conjunto de los números naturales N y el conjunto de los números pares P es el conjunto de los números que no son pares, es decir, los impares I
Complemento:
El complemento de un conjunto dado es otro conjunto que contiene todos los elementos que no están en el conjunto original.

RESUMEN:





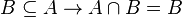

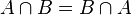

No hay comentarios:
Publicar un comentario