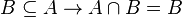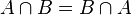Una expresión algebraica que involucra solamente operaciones de suma, resta, multiplicación y el elevar a potencias de números naturales son variables ( las letras) y constantes( números solitos) se llama polinomios.
Algunos ejemplos son:
5a + b 3x3 - 2x + 5
2x - 5y 9x2 - 8
x2 5x4 - 3x3 + x2 - x + 5
En un polinomio, la variable no puede aparecer en el denominador, como exponente ni dentro de un radical.
1
x No es un monomio porque la variable aparece en el denominador.
Un término es una expresión que está separada por los signos de suma o resta.
Ejemplos de términos: 3x , -2x2, 4
Un constante es un término que no contiene variables, solamente posee coeficiente.
Un monomio es un polinomio con un término.
5x3 Es un monomio
Los términos de un polinomio en una variable se arreglan usualmente de modo que los exponentes de la variable van en orden de mayor a menor y de izquierda a derecha. Esto se llama orden descendente.
4x3 - 3x2 + 6x - 1
5y4 - 2y3 + y2 - 7y + 8
El grado de un polinomio es el exponente mayor de la variable.
El Polinomio de 4x3 -3x2 + 6x - 1 es de grado 3
5y4 - 2y3 + y2- 7y + 8 es un polinomio de grado 4
domingo, 25 de octubre de 2015
Teoría de conjuntos
Un conjunto es la reunión en un todo de objetos bien definidos y diferenciables entre si, que se llaman elementos del mismo.
Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A.
En caso contrario, si a no es un elemento de A se denota aÏ A.
EJEMPLOS
Æ : el conjunto vacío, que carece de elementos.
ℕ: el conjunto de los números naturales.
ℤ: el conjunto de los números enteros.
ℚ: el conjunto de los números racionales.
ℝ: el conjunto de los números reales.
U: el conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal
Un conjunto se puede definir:
Por extensión: teniendo todos los conjuntos
Por compresión: mediante una propiedad
Subconjunto: En las matemáticas, un conjunto A es subconjunto de un conjunto B si A «está contenido» dentro de B.
AÍB

UNIÓN: Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B,
A È B := { x | x Î A Ú x Î B}.
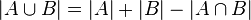

INTERSECCIÓN:
Dados dos conjuntos A y B, su intersección es otro conjunto cuyos elementos, necesariamente, pertenecen a los dos conjuntos A y B.
A Ç B := {x | x Î A Ù x Î B}
PROPIEDADES
Idempotencia. La intersección de un conjunto A consigo mismo es el propio A :
La intersección de A y B es un subconjunto de ambos:
La intersección de un conjunto B con un conjunto A que lo contenga, deja a B inalterado:
Propiedad asociativa: La intersección de los conjuntos A y B ∩ C es igual a la intersección de los conjuntos A ∩ B y C :
Propiedad conmutativa. La intersección de los conjuntos A y B es igual a la intersección de los conjuntos B y A :
Elemento absorvente. La intersección de un conjunto A con el conjunto vacío ∅ es ∅:

Diferencia:
La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.

EJEMPLO: la diferencia entre el conjunto de los números naturales N y el conjunto de los números pares P es el conjunto de los números que no son pares, es decir, los impares I
Complemento:
El complemento de un conjunto dado es otro conjunto que contiene todos los elementos que no están en el conjunto original.


RESUMEN:

Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A.
En caso contrario, si a no es un elemento de A se denota aÏ A.
EJEMPLOS
Æ : el conjunto vacío, que carece de elementos.
ℕ: el conjunto de los números naturales.
ℤ: el conjunto de los números enteros.
ℚ: el conjunto de los números racionales.
ℝ: el conjunto de los números reales.
U: el conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal
Un conjunto se puede definir:
Por extensión: teniendo todos los conjuntos
Por compresión: mediante una propiedad
Subconjunto: En las matemáticas, un conjunto A es subconjunto de un conjunto B si A «está contenido» dentro de B.
AÍB

UNIÓN: Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B,
A È B := { x | x Î A Ú x Î B}.
PROPIEDADES
Idempotencia. La unión de un conjunto A consigo mismo es el propio A :
- La unión de un conjunto A con un subconjunto suyo B lo deja inalterado:

Propiedad distributiva
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto: A ∪ (A ∩ B) = A
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto: A ∩ (A ∪ B) = A
Cardinalidad
El número de elementos de la unión de dos conjuntos finitos A y B es la suma de los elementos de A y de B, si no tienen elementos en común.

Como en un conjunto los elementos no pueden repetirse, si A y B tienen elementos en común, al sumar sus elementos se contarían los elementos comunes más de una vez.
Por ello, es necesario eliminar las repeticiones al contar los elementos de A ∪ B: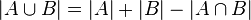
INTERSECCIÓN:
Dados dos conjuntos A y B, su intersección es otro conjunto cuyos elementos, necesariamente, pertenecen a los dos conjuntos A y B.
A Ç B := {x | x Î A Ù x Î B}
PROPIEDADES
Idempotencia. La intersección de un conjunto A consigo mismo es el propio A :
La intersección de A y B es un subconjunto de ambos:
La intersección de un conjunto B con un conjunto A que lo contenga, deja a B inalterado:
Propiedad asociativa: La intersección de los conjuntos A y B ∩ C es igual a la intersección de los conjuntos A ∩ B y C :
Propiedad conmutativa. La intersección de los conjuntos A y B es igual a la intersección de los conjuntos B y A :
Elemento absorvente. La intersección de un conjunto A con el conjunto vacío ∅ es ∅:
Propiedad distributiva
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto: A ∪ (A ∩ B) = A
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto: A ∩ (A ∪ B) = A
Diferencia:
La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.

EJEMPLO: la diferencia entre el conjunto de los números naturales N y el conjunto de los números pares P es el conjunto de los números que no son pares, es decir, los impares I
Complemento:
El complemento de un conjunto dado es otro conjunto que contiene todos los elementos que no están en el conjunto original.

RESUMEN:

Terna Pitagórica
Una terna pitagórica consiste en una tupla de tres enteros positivos a, b, c que cumplen que a² + b² = c². El nombre deriva del terorema de Pitágoras, el cual plantea que en cualquier triángulo rectángulo, se cumple que x² + y² = z² (siendo x e y las longitudes enteras de sus catetos y z la de la hipotenusa). En sentido contrario también se cumple, o sea, cualquier terna pitagórica se puede asociar con las longitudes de dos catetos y una hipotenusa, formando un triángulo rectángulo.
CÓMO HALLAR MÁS TERNAS PITAGÓRICAS
m,n Î ℕ
x = m² − n², y = 2mn, z = m² + n² x² + y² = z²Þ(m2+n2)2=(m2-n2)2+4mn
Si m=n darían soluciones triviales
EJEMPLO m=1 n=1 x=0 y=2 Z=2
CÓMO HALLAR MÁS TERNAS PITAGÓRICAS
m,n Î ℕ
Números trascendentes
Los números trascendentes son los números reales que no son solución de ninguna ecuación polinómica de coeficientes racionales. Por lo que hemos visto antes todos los números trascendentes son irracionales, aunque no todos los irracionales son trascendentes. Como ejemplos más representativos de este conjunto numérico tenemos al número π y al número  .
.
Viendo que en primera instancia es mucho más sencillo encontrar números algebraicos que números trascendentes uno podría pensar que hay muchos más del primer tipo que del segundo. Nada más lejos de la realidad. El conjunto de los números algebraicos es infinito numerable, es decir, tiene infinitos elementos pero podemos contarlos, mientras que el conjunto de los números trascendentes es infinito no numerable, esto es, también tiene infinitos elementos pero no los podemos contar. Conclusión: hay muchos más números reales trascendentes que algebraicos.
La existencia de los números trascendentes fue finalmente probada en 1844 por Joseph Liouville, en 1851 mostró ejemplos entre los que estaba la "Constante de Liouville", donde el enésimo dígito después de la coma decimal es 1 si n es un factorial (es decir, 1, 2, 6, 24, 720, etc.) y 0 en cualquier caso.
Números algebraicos
Los número algebraicos son los números reales que son solución de alguna ecuación polinómica cuyos coeficientes son números racionales. A la vista de esta definición es fácil comprender que todos los números racionales son algebraicos, ya que si  es un número racional (por tanto
es un número racional (por tanto  ), entonces
), entonces  es solución de la ecuación polinómica
es solución de la ecuación polinómica  .
.
domingo, 18 de octubre de 2015
Generalización
¿Qué es la generalización?
Es pasar de un concepto (fórmula, proposición...etc) limitado a otro más extenso que lo contenga.
Generalizar:
a) a=bÛa2=b2
a=bÛan=bn
b) x2+y2=z2
xn+yn=zn
c)
Es pasar de un concepto (fórmula, proposición...etc) limitado a otro más extenso que lo contenga.
Generalizar:
a) a=bÛa2=b2
a=bÛan=bn
b) x2+y2=z2
xn+yn=zn
c)
Proposiciones matemáticas
¿Qué es una proposición matemática?
Es un contenido semántico al que se le ha asignado uno de los posibles valores verdaderos y falsos.
PÞQ
Hay dos tipos:
-Implicación, P sería la causa y Q el efecto.
Ej. PÞQ y se interpreta,"Si P, entonces Q".
-Doble implicación, P sería verdad solamente cuando Q también lo sea.
Ej. PÛQ y se interpreta, "P si y solo si Q".
PÛQ= (PÞQ)Ù(QÞP)
También se pueden distinguir:
Proposición directa, es la proposición que enunciamos. Ej. PÞQ
Proposición contraria, es la proposición que niega a la directa. Ej. NoPÞNoQ
Proposición recíproca, es la proposición inversa a la directa. Ej. QÞP
Proposición contrarrecíproca. es la proposición que niega a la recíproca. Ej. NoQÞNoP
Ejercicio, pon las proposiciones contraria, recíproca y contrarrecíproca de esta afirmación:
-Si -n- es impar y -m- es impar entonces n+m es par.
-Contraria: Si -n- no es impar o -m- no es impar entonces n+m no es par.
-Recíproca: Si n+m es par entonces -n- es impar y -m- es impar.
-Contrarrecíproca: Si n+m no es impar entonces -n- no es impar o -m- no es impar.
Toda proposición que sea verdadera necesita una demostración.
Ej. a=bÞa2=b2
Demostración: a2=a·a=a·b=b·b=b2
Toda proposición que sea falsa requiere de un contraejemplo.
Ej. a2=b2Þa=b
Contraejemplo: (–3)2=32Þ–3≠3
Es un contenido semántico al que se le ha asignado uno de los posibles valores verdaderos y falsos.
PÞQ
Hay dos tipos:
-Implicación, P sería la causa y Q el efecto.
Ej. PÞQ y se interpreta,"Si P, entonces Q".
-Doble implicación, P sería verdad solamente cuando Q también lo sea.
Ej. PÛQ y se interpreta, "P si y solo si Q".
PÛQ= (PÞQ)Ù(QÞP)
También se pueden distinguir:
Proposición directa, es la proposición que enunciamos. Ej. PÞQ
Proposición contraria, es la proposición que niega a la directa. Ej. NoPÞNoQ
Proposición recíproca, es la proposición inversa a la directa. Ej. QÞP
Proposición contrarrecíproca. es la proposición que niega a la recíproca. Ej. NoQÞNoP
Ejercicio, pon las proposiciones contraria, recíproca y contrarrecíproca de esta afirmación:
-Si -n- es impar y -m- es impar entonces n+m es par.
-Contraria: Si -n- no es impar o -m- no es impar entonces n+m no es par.
-Recíproca: Si n+m es par entonces -n- es impar y -m- es impar.
-Contrarrecíproca: Si n+m no es impar entonces -n- no es impar o -m- no es impar.
Toda proposición que sea verdadera necesita una demostración.
Ej. a=bÞa2=b2
Demostración: a2=a·a=a·b=b·b=b2
Toda proposición que sea falsa requiere de un contraejemplo.
Ej. a2=b2Þa=b
Contraejemplo: (–3)2=32Þ–3≠3
viernes, 16 de octubre de 2015
Radicales
miércoles, 7 de octubre de 2015
Descubriendo cosas nuevas
Estamos repasando los números decimales. Nuestro profesor aparentemente nos dijo una mentira de primeras, que era que los números decimales exactos también eran periódicos, parece falso, pero todos los números "exactos" tienen un número infinito de 0, luego es periódico. Dicho esto se deduce que todos los números racionales también se pueden llamar números decimales periódicos, y los irracionales números decimales no periódicos.
Primeros días
Para realizar un camino tenemos que dar los primeros pasos. En matemáticas pasa igual.
Nuestro profesor nos está enseñando un aspecto de las matemáticas que ningún otro profesor nos ha enseñado; leer el lenguaje matemático. Un sencillo aspecto como saber leer una fórmula, el significado de los signos etc. Como por ejemplo ^ significa -y-, otro caso similar pasa con v que es -o-.
Otro aspecto es la utilización de proposiciones:
-Proposición directa (la enunciada). Ej. P=>Q
-Proposición contraria (negar la directa). Ej. NoP=>NoQ
-Proposición recíproca (la inversa a la directa). Ej. Q=>P
-Proposición contrarrecíproca (negar la recíproca). Ej. NoQ=>NoP
Nuestro profesor nos está enseñando un aspecto de las matemáticas que ningún otro profesor nos ha enseñado; leer el lenguaje matemático. Un sencillo aspecto como saber leer una fórmula, el significado de los signos etc. Como por ejemplo ^ significa -y-, otro caso similar pasa con v que es -o-.
Otro aspecto es la utilización de proposiciones:
-Proposición directa (la enunciada). Ej. P=>Q
-Proposición contraria (negar la directa). Ej. NoP=>NoQ
-Proposición recíproca (la inversa a la directa). Ej. Q=>P
-Proposición contrarrecíproca (negar la recíproca). Ej. NoQ=>NoP
PRÓLOGO
Este blog estará dedicado al aprendizaje de mí y mi clase en las matemáticas, relatando los aspectos más relevantes de este largo y duro camino académico.
Suscribirse a:
Comentarios (Atom)