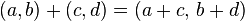ELEMENTOS DE UN VECTOR
Dirección de un vector: Está representado por la recta que contiene al vector .se define como el ángulo que hace dicho vector con una o más rectas de referencia , según sea el caso en el plano o en el espacio.
Sentido de un vector: Indica la orientación de un vector, gráficamente está dado por la cabeza de la flecha del vector.
Módulo de un vector: Representa el valor de la cantidad física vectorial, está representado por la longitud del vector, tomado o medido a cierta escala.
VECTOR FIJO: pareja ordenada de puntos en el plano

VECTOR LIBRE
RELACIÓN DE EQUIPOLENCIA: Dos vectores son equipolentes si tienen la misma dirección, módulo y sentido.

La equivalencia es una clase de equivalencia en que se deben de cumplir las 3 propiedades, la clase de equivalencia también se llama vector libre.



REPRESENTACIÓN DE UN VECTOR LIBRE

OPERACIONES
SUMA
Hay 2 formas:
1ª Dados 2 vectores colocar uno en el extremo del otro

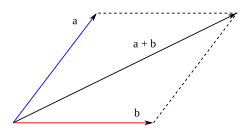
2ª Utilizando la regla del paralelogramo
PROPIEDADES






Dirección de un vector: Está representado por la recta que contiene al vector .se define como el ángulo que hace dicho vector con una o más rectas de referencia , según sea el caso en el plano o en el espacio.
Sentido de un vector: Indica la orientación de un vector, gráficamente está dado por la cabeza de la flecha del vector.
Módulo de un vector: Representa el valor de la cantidad física vectorial, está representado por la longitud del vector, tomado o medido a cierta escala.
VECTOR FIJO: pareja ordenada de puntos en el plano
VECTOR LIBRE
RELACIÓN DE EQUIPOLENCIA: Dos vectores son equipolentes si tienen la misma dirección, módulo y sentido.
La equivalencia es una clase de equivalencia en que se deben de cumplir las 3 propiedades, la clase de equivalencia también se llama vector libre.
La relación de equipolencia cumple las siguientes propiedades:
1) Reflexiva
Todo vector fijo es equipolente a sí mismo.
2) Simétrica
Si un vector es equipolente a otro, este es equipolente a aquel.
3) Transitiva
Si un vector es equipolente a otro y este lo es a un tercero, el primero es equipolente al tercero.
REPRESENTACIÓN DE UN VECTOR LIBRE
OPERACIONES
SUMA
Hay 2 formas:
1ª Dados 2 vectores colocar uno en el extremo del otro
2ª Utilizando la regla del paralelogramo

PROPIEDADES
Propiedad conmutativa: El orden de los sumandos no altera el resultado
Propiedad asociativa: Propiedad que establece que cuando se suman tres o mas vectores, la suma siempre es la misma independientemente de su agrupamiento.
Vector nulo: Existe un vector que actúa como elemento nulo y cuando cualquier vector se sume con este vector el resultado es el mismo vector original.
0+a=a
Vector opuesto: Para cualquier vector a, existe un vector −a tal que a+(-a) = 0. Este vector −a se denomina vector opuesto, y es único para cada a.
RESTA
PRODUCTO POR ESCALAR
El producto de un número k por un vector  es otro vector:
es otro vector:
De igual dirección que el vector  .
.
Del mismo sentido que el vector  si k es positivo.
si k es positivo.
De sentido contrario del vector  si k es negativo.
si k es negativo.
De módulo 
VECTOR UNITARIO
Un vector unitario es un vector de módulo uno. En ocasiones se le llama también vector normalizado.
COMBINACIÓN LINEAL DE VECTORES
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por sendos escalares.
VECTOR ORTOGONAL
Dos vectores son ortogonales o perpendiculares si su producto escalar es cero.
SISTEMA DE VECTORES: un subconjunto de vectores
SISTEMA LIBRE DE VECTORES
Sistema de vectores en el que el vector nulo se puede representar como una única combinación lineal.
Si un sistema es libre y le quito un vector, el nuevo sistema sigue siendo libre.
Un sistema formado por un vector no nulo, es siempre libre.
Si ese vector es nulo, será un sistema ligado.
SISTEMA LIGADO: sistema de vectores en el que el vector se puede expresar de varias formas.
SISTEMA LIBRE MAXIMAL
Sistema libre en el que al añadir un vector deja de ser libre.