lunes, 16 de mayo de 2016
miércoles, 20 de abril de 2016
Infinitos e infinitésimos
INFINITOS
Una función se dice infinito en un x0 si lim f (x) = ±∞ .
Ejemplos:
1/x2 en x=0
x en +∞
x3 en -∞
INFINITÉSIMOS
Una función se dice infinitésimo en x0 si lim f (x) = 0
Ejemplos:
1/x en +∞
x2 en 0
sen0 en 0
COMPARACIÓN DE INFINITOS
Dos funciones f y g infinitas en x0 se pueden comparar mediante el uso del cociente entre ellas.
lim f (x) = ±∞
lim g (x) = ±∞
lim f (x)/g(x) = se crea una indeterminación de ∞/∞, que resolviéndose se pueden dar tres casos, si su límite es ±∞, si su límite es un número real o si su límite es 0.
Si su límite es +∞, f es de orden superior
Si su límite es 0, g es de orden superior
Si su límite es un número real, ambas son del mismo orden
Si su límite es 1, son infinitos equivalentes
Ejemplo:
f(x)=3x2+2x+-1
g(x)=3x2
lim3x2+2x+-1/3x2=∞/∞=1
Para calcular el límite en el caso de un producto o cociente si un factor es infinito puedo sustituirlo por un infinito equivalente.
lim3x2+2x+-1/-2x3+5x-3=3x2/-2x3=0
COMPARACIÓN DE INFINITÉSIMOS
Dos funciones f y g infinitésimas en x0 se pueden comparar mediante el uso del cociente entre ellas.
lim f (x) = 0
lim g (x) = 0
lim f (x)/g(x) = se crea una indeterminación de 0/0, que resolviéndose se pueden dar tres casos, si su límite es ±∞, si su límite es un número real o si su límite es 0.
Para calcular el límite en el caso de un producto o cociente si un factor es infinitésimo puedo sustituirlo por un infinito equivalente.
Una función se dice infinito en un x0 si lim f (x) = ±∞ .
Ejemplos:
1/x2 en x=0
x en +∞
x3 en -∞
INFINITÉSIMOS
Una función se dice infinitésimo en x0 si lim f (x) = 0
Ejemplos:
1/x en +∞
x2 en 0
sen0 en 0
COMPARACIÓN DE INFINITOS
Dos funciones f y g infinitas en x0 se pueden comparar mediante el uso del cociente entre ellas.
lim f (x) = ±∞
lim g (x) = ±∞
lim f (x)/g(x) = se crea una indeterminación de ∞/∞, que resolviéndose se pueden dar tres casos, si su límite es ±∞, si su límite es un número real o si su límite es 0.
Si su límite es +∞, f es de orden superior
Si su límite es 0, g es de orden superior
Si su límite es un número real, ambas son del mismo orden
Si su límite es 1, son infinitos equivalentes
Ejemplo:
f(x)=3x2+2x+-1
g(x)=3x2
lim3x2+2x+-1/3x2=∞/∞=1
Para calcular el límite en el caso de un producto o cociente si un factor es infinito puedo sustituirlo por un infinito equivalente.
lim3x2+2x+-1/-2x3+5x-3=3x2/-2x3=0
COMPARACIÓN DE INFINITÉSIMOS
Dos funciones f y g infinitésimas en x0 se pueden comparar mediante el uso del cociente entre ellas.
lim f (x) = 0
lim g (x) = 0
lim f (x)/g(x) = se crea una indeterminación de 0/0, que resolviéndose se pueden dar tres casos, si su límite es ±∞, si su límite es un número real o si su límite es 0.
Para calcular el límite en el caso de un producto o cociente si un factor es infinitésimo puedo sustituirlo por un infinito equivalente.
domingo, 31 de enero de 2016
Geometría vectorial del plano
ELEMENTOS DE UN VECTOR
Dirección de un vector: Está representado por la recta que contiene al vector .se define como el ángulo que hace dicho vector con una o más rectas de referencia , según sea el caso en el plano o en el espacio.
Sentido de un vector: Indica la orientación de un vector, gráficamente está dado por la cabeza de la flecha del vector.
Módulo de un vector: Representa el valor de la cantidad física vectorial, está representado por la longitud del vector, tomado o medido a cierta escala.
VECTOR FIJO: pareja ordenada de puntos en el plano

VECTOR LIBRE
RELACIÓN DE EQUIPOLENCIA: Dos vectores son equipolentes si tienen la misma dirección, módulo y sentido.

La equivalencia es una clase de equivalencia en que se deben de cumplir las 3 propiedades, la clase de equivalencia también se llama vector libre.



REPRESENTACIÓN DE UN VECTOR LIBRE

OPERACIONES
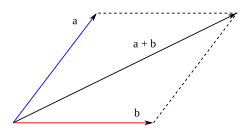
SUMA
Hay 2 formas:
1ª Dados 2 vectores colocar uno en el extremo del otro

2ª Utilizando la regla del paralelogramo
PROPIEDADES






Dirección de un vector: Está representado por la recta que contiene al vector .se define como el ángulo que hace dicho vector con una o más rectas de referencia , según sea el caso en el plano o en el espacio.
Sentido de un vector: Indica la orientación de un vector, gráficamente está dado por la cabeza de la flecha del vector.
Módulo de un vector: Representa el valor de la cantidad física vectorial, está representado por la longitud del vector, tomado o medido a cierta escala.
VECTOR FIJO: pareja ordenada de puntos en el plano
VECTOR LIBRE
RELACIÓN DE EQUIPOLENCIA: Dos vectores son equipolentes si tienen la misma dirección, módulo y sentido.
La equivalencia es una clase de equivalencia en que se deben de cumplir las 3 propiedades, la clase de equivalencia también se llama vector libre.
La relación de equipolencia cumple las siguientes propiedades:
1) Reflexiva
Todo vector fijo es equipolente a sí mismo.
2) Simétrica
Si un vector es equipolente a otro, este es equipolente a aquel.
3) Transitiva
Si un vector es equipolente a otro y este lo es a un tercero, el primero es equipolente al tercero.
REPRESENTACIÓN DE UN VECTOR LIBRE
OPERACIONES
SUMA
Hay 2 formas:
1ª Dados 2 vectores colocar uno en el extremo del otro
2ª Utilizando la regla del paralelogramo

PROPIEDADES
Propiedad conmutativa: El orden de los sumandos no altera el resultado
Propiedad asociativa: Propiedad que establece que cuando se suman tres o mas vectores, la suma siempre es la misma independientemente de su agrupamiento.
Vector nulo: Existe un vector que actúa como elemento nulo y cuando cualquier vector se sume con este vector el resultado es el mismo vector original.
0+a=a
Vector opuesto: Para cualquier vector a, existe un vector −a tal que a+(-a) = 0. Este vector −a se denomina vector opuesto, y es único para cada a.
RESTA
PRODUCTO POR ESCALAR
El producto de un número k por un vector  es otro vector:
es otro vector:
De igual dirección que el vector  .
.
Del mismo sentido que el vector  si k es positivo.
si k es positivo.
De sentido contrario del vector  si k es negativo.
si k es negativo.
De módulo 
VECTOR UNITARIO
Un vector unitario es un vector de módulo uno. En ocasiones se le llama también vector normalizado.
COMBINACIÓN LINEAL DE VECTORES
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por sendos escalares.
VECTOR ORTOGONAL
Dos vectores son ortogonales o perpendiculares si su producto escalar es cero.
SISTEMA DE VECTORES: un subconjunto de vectores
SISTEMA LIBRE DE VECTORES
Sistema de vectores en el que el vector nulo se puede representar como una única combinación lineal.
Si un sistema es libre y le quito un vector, el nuevo sistema sigue siendo libre.
Un sistema formado por un vector no nulo, es siempre libre.
Si ese vector es nulo, será un sistema ligado.
SISTEMA LIGADO: sistema de vectores en el que el vector se puede expresar de varias formas.
SISTEMA LIBRE MAXIMAL
Sistema libre en el que al añadir un vector deja de ser libre.
viernes, 29 de enero de 2016
Entrevista
_¿Cuál es el motivo de su devoción hacia las matemáticas?
_¿Por qué la Cuadratura mediante interpolación en métodos
Galerkin no lineales?
_¿Qué supuso su breve estancia en Dundee?
_¿Hay algún otro campo científico que le hubiera gustado
estudiar?
_¿Qué le diría a una persona que no valora a las matemáticas
para mostrarle la importancia de las mismas en la vida?
_¿Cómo han cambiado los métodos de enseñanza de la materia
en estos últimos años?
_¿En qué aspectos se han avanzado en las matemáticas en estos
últimos años?
_¿Piensa qué es correcta la manera en que se imparten las
clases de matemáticas en los institutos españoles? ¿Si no está de a favor de la
misma, cual sería la mejor manera de impartir las clases?
domingo, 24 de enero de 2016
Números Complejos
Los números complejos son una extensión de los números reales. El conjunto de los números complejos se designa con la notación  , siendo
, siendo  el conjunto de los números reales se cumple que
el conjunto de los números reales se cumple que  . Todo número complejo puede representarse como la suma de un número real y un número imaginario. Al número a + bi le llamamos número complejo en forma binómica.El número a es la parte real del número complejo.El número b es la parte imaginaria del número complejo.Si b = 0 el número complejo se reduce a un número real ya que a + 0i =a. Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
. Todo número complejo puede representarse como la suma de un número real y un número imaginario. Al número a + bi le llamamos número complejo en forma binómica.El número a es la parte real del número complejo.El número b es la parte imaginaria del número complejo.Si b = 0 el número complejo se reduce a un número real ya que a + 0i =a. Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
Los números complejos a + bi y -a -bi se llaman opuestos.
 , siendo
, siendo  el conjunto de los números reales se cumple que
el conjunto de los números reales se cumple que  . Todo número complejo puede representarse como la suma de un número real y un número imaginario. Al número a + bi le llamamos número complejo en forma binómica.El número a es la parte real del número complejo.El número b es la parte imaginaria del número complejo.Si b = 0 el número complejo se reduce a un número real ya que a + 0i =a. Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
. Todo número complejo puede representarse como la suma de un número real y un número imaginario. Al número a + bi le llamamos número complejo en forma binómica.El número a es la parte real del número complejo.El número b es la parte imaginaria del número complejo.Si b = 0 el número complejo se reduce a un número real ya que a + 0i =a. Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.Los números complejos a + bi y -a -bi se llaman opuestos.
Conjugado de un número complejo
Dos binomios se llaman conjugados si solo difieren en su signo central. De esta manera, el conjugado de un complejo zes un nuevo número complejo, definido así:

- Representación
- OPERACIONES
- Suma
-
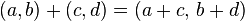
- Multiplicación

- PROPIEDADES
- Propiedad conmutativa: z+w = w+z; zw= wz.
- Propiedad asociativa: v+(w+z)= (v+w)+ z; v(wz)= (vw)z
- Propiedad distributiva: v(w+z) = vw+vz; (w+z)v = wv+zv
- Existencia de identidades:
- La identidad aditiva, el cero: z+ 0 = 0+z = z; la identidad multiplicativa, el 1:

- Inversos: cada número complejo tiene su inverso aditivo -z tal que z +(-z) = 0 y cada número complejo, distinto de cero, tiene su inverso multiplicativo z-1, tal que z·z-1 = 1.
jueves, 7 de enero de 2016
¿Por qué se sincronizan los metrónomos?
Si colocas 32 metrónomos sobre un objeto estático y rígido y los pones a funcionar desincronizados entre ellos, se quedarán así indefinidamente. Pero si los colocas sobre una superficie móvil, algo realmente interesante e hipnotizador sucede.
Los metrónomos de este vídeo son un ejemplo del segundo caso. La energía del movimiento de uno de los metrónomos afecta al movimiento de todos los demás metrónomos de su alrededor, mientras que la energía del movimiento de todos los demás metrónomos afecta al movimiento de nuestro metrónomo original. Toda esta comunicación ínter-metrónomo es facilitada por la tabla sobre la que descansan, que hace las funciones de intermediario energético entre todos los metrónomos colocados sobre ella. Los metrónomos de este vídeo (en realidad son sencillamente péndulos) están abocados a sincronizarse.
Es una metáfora que refleja que la mayoría influye en el comportamiento del individuo, ya que la sociedad es versátil, flexible y cambiante. Aunque también puede explicarse, como que el comportamiento del individuo es capaz de cambiar a la sociedad, siempre y cuando nos encontremos en una sociedad con libertad de expresión...,ya que en este caso nuestro comportamiento quedaría delimitado por el régimen.
Ejercicio 2
Se quiere reconstruir la ubicación y las dimensiones de un claustro de forma cuadrada desaparecido y del que se ha encontrado su pozo. Se tienen dudas de la ubicación del pozo en relación al claustro pero se sabe que dicho pozo distaba 30, 40 y 50 m de las esquinas del claustro.
Nos decidimos a resolver el problema mediante el teorema del coseno, pues no poseemos todos los lados y solo tenemos un ángulo.
Ya que cos(90-α)=senα

La segunda solución es válida matemáticamente, pero no tiene sentido en este problema, puesto que entonces, el pozo quedaría fuera del claustro.
Ejercicio 3
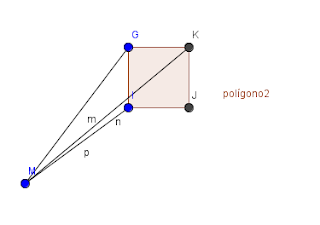
Una barra de longitud constante AB se desliza sobre una semicircunferencia, de modo que sus extremos A y B están siempre sobre la semicircunferencia. En cada posición de la barra proyectamos los extremos de la misma sobre el diámetro de la semicircunferencia y construimos el triángulo de vértices MPR, siendo M el punto medio de la barra. ¿Cómo evoluciona este triángulo?
-Elabora una construcción dinámica con GEOGEBRA que permita ver dicha evolución.
- Demuestra, utilizando el teorema de Tales, que el triángulo MPR es isósceles.
- Como el segmento AB se desliza por la semicircunferencia, el triángulo MPR varía, demuestra que cualquiera de esos triángulos MPR son semejantes.
Siempre serán semejantes ya que la altura y la base disminuyen y aumentan proporcionalmente.
-Elabora una construcción dinámica con GEOGEBRA que permita ver dicha evolución.
- Demuestra, utilizando el teorema de Tales, que el triángulo MPR es isósceles.
- Como el segmento AB se desliza por la semicircunferencia, el triángulo MPR varía, demuestra que cualquiera de esos triángulos MPR son semejantes.
Siempre serán semejantes ya que la altura y la base disminuyen y aumentan proporcionalmente.
Esta tierra es mía
Esta tierra es
mía es una película de 1943 dirigida por Jean Renoir e
interpretada por Charles Laughton, Maureen O'Hara, George
Sanders y Walter Slezak en sus papeles principales.
En una ciudad de la
Francia ocupada, Albert Lory (Charles Laughton), un
maestro solterón, que vive con su madre, a raíz de su actitud en los bombardeos
ha adquirido fama, incluso entre sus alumnos, de persona de poco aplomo. Oculta
su amor por otra profesora, compañera y vecina suya, Louise Martin (Maureen O'Hara),
conformándose con su amistad y la de su hermano Paul. Además, ella mantiene relaciones
sentimentales con George Lambert (George Sanders), por lo que la ve inalcanzable. Paul es
miembro de la resistencia francesa y muy activo en las labores de sabotaje, por
ello, es traicionado por George que lo delata a los nazis, ya que entiende que
la colaboración es el único medio de alcanzar la paz. Albert, en un arrebato de
indignación, se dirige al encuentro de George justo en el momento en que este,
arrepentido, comete suicidio. Albert, es acusado injustamente de asesinato.
Durante el juicio, Albert, investido de una serena dignidad y un valor desconocido
por todos, dirige un memorable alegato de la libertad que enciende a sus
conciudadanos. Advirtiendo el peligro de sublevación, el comandante nazi, el
Mayor Erich von Keller, le propone un trato: si cesa en su alegato y depone su
actitud en el juicio, le garantiza un veredicto de inocencia. De regreso al
tribunal, Albert continúa en su actitud y arenga a sus conciudadanos.
El argumento presenta bastante
profundidad acercándose, a través de unos personajes muy bien construidos, a la
realidad de lo que fueron las zonas ocupadas durante la II Guerra Mundial. Se
muestran con naturalidad, sin dejar de juzgarlos negativamente, personajes que
abiertamente colaboran con los nazis para obtener un provecho personal. Por
ejemplo el Alcalde y los comerciantes que se lucran con la situación sin pasar
necesidad como los demás. El personaje del jefe de estación que colabora en un
principio para no tener problemas con los alemanes, va evolucionando y pasa de
ser un nazi idealista a justificar su colaboración para evitar que inocentes
paguen por las acciones de otros. Su arrepentimiento le llevará a avisar al
saboteador antes de su detención tras haberlo delatado, y al suicidio cuando se
ve atrapado por el Mayor Von Keller como colaborador sin remedio. El personaje del Sr. Lory
interpretado por Charles Laughton es la auténtica joya de esta película que
hace que no haya pasado desapercibida como una cinta más sobre la ocupación. El
alegato final de Laughton en el juicio donde arroja su cobardía a sus
convecinos y al ocupante alemán. Todo un canto a la Libertad en una
interpretación inolvidable. Es muy poco creíble que Maureen O’Hara se enamore
por las buenas de Lory sólo por su gran demostración de valor en el juicio.
Aunque carece casi
por completo de acción, se trata de una obra maestra del cine bélico y de un
gran canto a la libertad. Muy recomendable.
Suscribirse a:
Comentarios (Atom)


















